ゲームの話

　ふぞろいメンバーのミーティングは基本zoomで行われるのですが、昨今の情勢を受けて娘が参加する学校行事のミーティングもzoomで行うことになり、先日zoomの手ほどきをしました。久しぶりに娘に尊敬されてちょっと満足。

　みなさんこんにちは、「勉強は無理せず少しずつ」がモットーのアラフォー受験生応援団のヌワンコです。自己紹介はこちら。

　本日はゲームの話です。待望のFF7リメイクですが素晴らしい映像でしたね。一方Switchは品薄で全然買えません。

　違う、そうじゃない。

　一次試験「経済学・経済政策」の範囲である「ゲーム理論」のお話です。取り上げられることの少ないテーマですが、２次試験までを視野に入れると、覚えていて損はないテーマなのです。

ゲーム理論とは

　ゲーム理論とは「相手がある行動をしたら自分はどう行動するか」あるいは「自分がある行動をしたら相手はどう行動するか」といった、お互いの意思決定・行動の相互依存関係を分析するモデルです。日常でも自分の意思決定や行動が、相手の意思決定や行動に影響を受けることがありますし、その逆もあるかと思います。
　診断士試験ではゲーム理論はミクロ経済学の寡占に関連して出題されることが多いですが、それ以外の社会的な事象や慣習を説明するのにも用いられます。

ゲーム理論で多くのことが説明できる

　私は関東圏の人間ですが、大阪に出張すると毎回うっかり新大阪駅でエスカレーターの左側に立ってしまいます。最近では「エスカレーターでは歩かない」という新たなマナーもありますが、関東と関西の文化の違いとしてよく言われますよね。
　歴史的な経緯はおいといて、なぜいまだに文化の相違は解消されずに関東では（関西の方も含めて）みな左側に立つのでしょうか？このことはゲーム理論の例としてよく取り上げられます。

　簡単にまとめると、他の人の行動を予想した結果、自分だけ右側に立って損（後ろからの無言の圧力）をしないよう自分の行動を決めているのです。そして一度「左側に立つ」と決まると、自分だけが行動を変えることによるメリットがないことから、その状態がずっと続きます。この状態を（細かな定義は別として）「ナッシュ均衡」と呼びます。

　それ以外にも「キーボード配列がQWERTY配列のままの理由」「トイレットペーパーの買占めが起こる理由」などの一見不合理に見える世の中の事象もゲーム理論で説明されます。

　では診断士試験の世界に戻って本題に入りましょう。ゲーム理論の基本は上で述べた「ナッシュ均衡」を確認することが出発点となります。
　ゲームには「同時ゲーム」「逐次ゲーム」の２つがあるので、それぞれ説明しますね。

ゲーム理論①：同時ゲーム

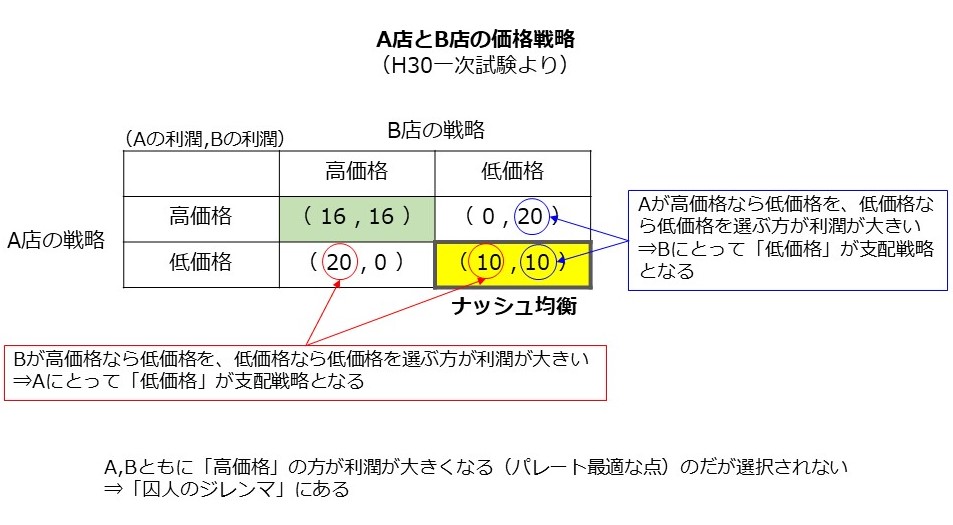
　同時ゲームとはじゃんけんのように「両者が同時に意思決定を行う」ゲームです。このゲームは下のような利得表で示されます。
　ナッシュ均衡を導くための手順は以下のとおりです。

（１） Aの立場になり、Bの選択肢（高価格/低価格）においてAの利得が大きい方に〇をつける。
（２） 今度はBの立場になり、Aのそれぞれの選択肢においてBの利得が大きい方に〇をつける。
（３） A、Bともに〇がついているのがナッシュ均衡。

　ナッシュ均衡の注意点は２つです。

【注意点１】「ナッシュ均衡」イコール「パレート最適」とは限らない
　パレート最適は余剰分析で出てきたかと思いますが「他の人の効用を下げない限り自分の効用を上げられない」状態です。上の図では「A,Bともに低価格」はナッシュ均衡ではありますがパレート最適ではありません。高価格にすることでAから見ればBの利益を上げながらA自身の利益を上げられるはず（逆も同様）なのですが、選択されません。
　このような状態を「囚人のジレンマ」と呼びます。２人の囚人を別の牢屋に閉じ込めるゲームを想定し、それぞれに黙秘と自白の選択肢を与えたところ、結果として双方自白を選んでしまう、ことから来ています。
　逆に言えば「もしも相互に連絡手段があり、黙秘で合意する」ことができれば利得が最大化できます。先ほどの価格戦略なら「双方が高価格とする」ことを取り決めることであり、企業間の協調的行動（カルテル等）の説明として用いられることもあります。

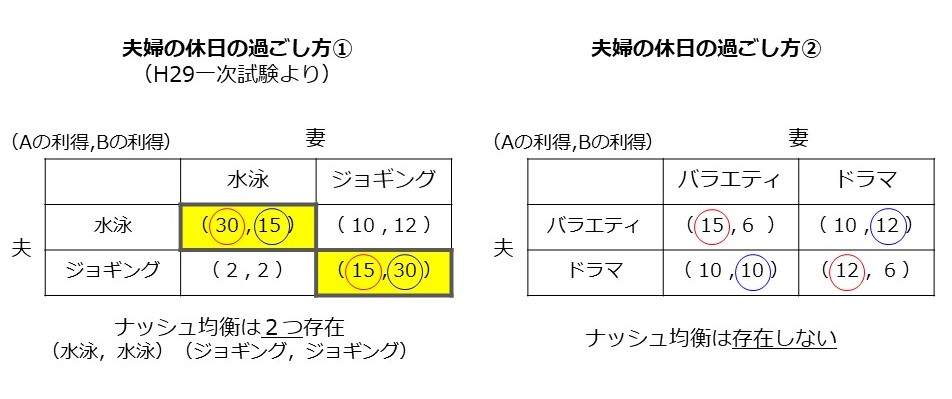
【注意点２】ナッシュ均衡は１つとは限らない
　左下の図ではナッシュ均衡が２つ存在しています。
　逆に右下の図のようにナッシュ均衡が存在しないパターンもあります。

ゲーム理論②：逐次ゲーム

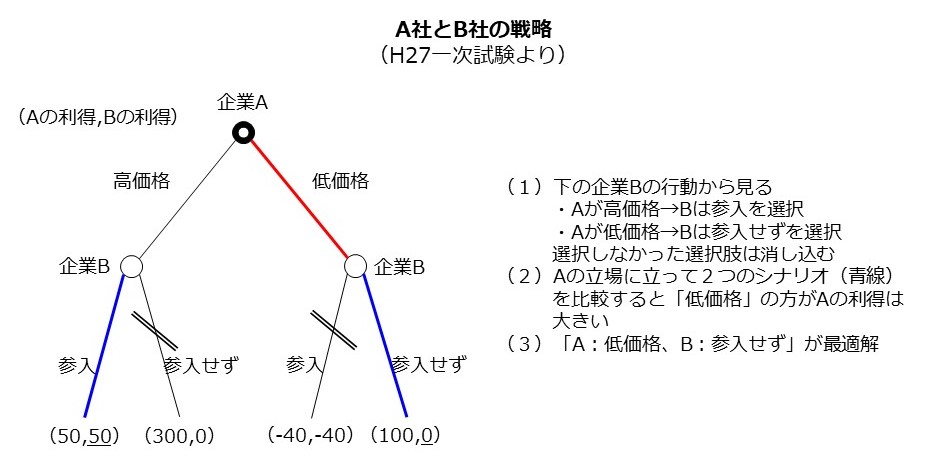
　オセロのような「BはAの行動を見てから自分の行動を決める」ゲームを逐次ゲームと呼びます。このゲームは下のような樹形図で表現されます（これを「ゲーム木」と呼びます）。
　さて逐次ゲームを解く場合には鉄則があります。それは「後ろ（の番）から解け」です。細かい理屈は割愛して、下の図を用いて手順を説明します。

（１） 先にBの行動から見る。Bは自分の利得が大きい方を選ぶので「Aが高価格の場合は参入」、「Aが低価格の場合は参入せず」を選択する。排除された選択肢には「／」をつけて閉じる。
（２） Aの行動を見る。Aは自分の利得が大きい「低価格」を選択する。
（３） Aは低価格戦略を採用してBは参入せず、が最適解になる。

　これを利得表で示した場合は下のようになります。利得表で導かれるナッシュ均衡は１つですが、A社の立場であればどう考えても選択しそうにない、信ぴょう性に欠ける均衡となっています。こうした信ぴょう性に欠ける解を排除するため、逐次ゲームは後ろから解く（バックワード・インダクション）ことになります。

２次試験との関連性

　最後に２次試験との関連性についてです。ゲームの木の考え方が、ディシジョンツリーに繋がっているといわれています。ですので、ディシジョンツリーを解く際も「後ろから解いていく」ことが手順になります。

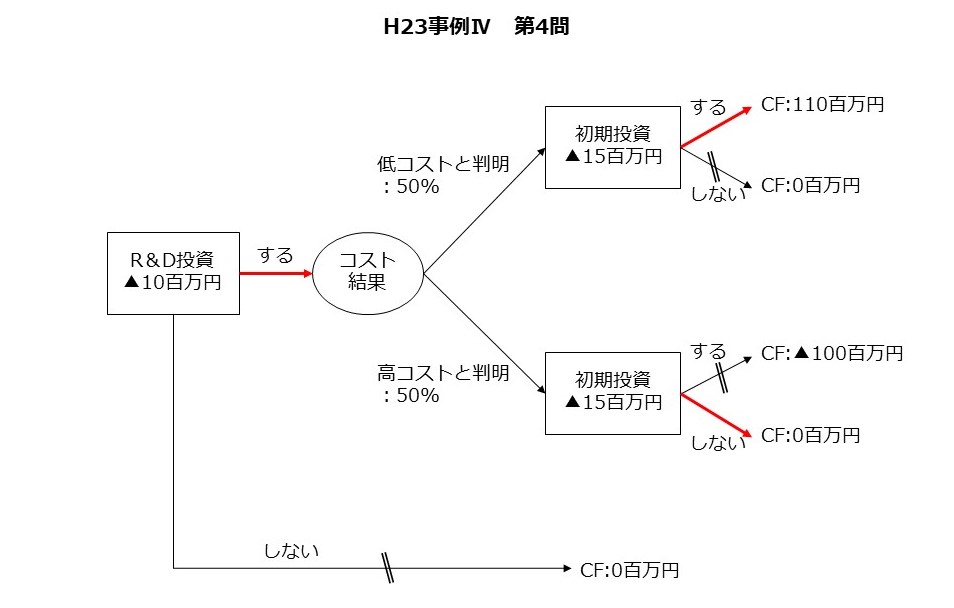
ディシジョンツリーは事例Ⅳでは頻出テーマではありませんが、手順さえ理解していれば計算は複雑ではない、という問題もあります。余裕のある方はおさらいをしておきましょう。

　さて明日は、ついにオリジナルの例題作成まで始めちゃってた（ビックリしたわ）かーなの登場です。